Psychological research often emphasizes statistic representations of individual characteristics. In developmental psychology, we are interested in how people change. Thus, the focus of our research should be on finding better ways to measure change or mechanisms of change. Representing the dynamics of an individual allows for measurement of variability, which is indicative of changes in psychological characteristic. Thus, the examination of intraindividual variability is a crucial component to understanding underlying processes. That is, we are interested in how an individual changes within the constraints of that individual’s environment. Once we know that information, we can then see interindividual change patterns.
How Should We Measure Change or Should We?
Cronbach and Furby (1970) title their seminal paper on change: “How we should measure change or should we?” The last line is quite interesting, “or should we?” Is change so difficult to measure that is is not worth our time? Cronbach and Furby presented the difficulties in measuring change and presented a potential alternative. Since that time, additional models of change have proposed. This paper will walk through some difficulties that we still face today and present a type of model that might get around these issues. This type of modeling may also allow us to find leading indicators of the change process that get at causal mechanisms. In combination with longitudinal research, we can get much closer to figuring out potential causal mechanisms.
Historical Methods of Measuring Change
Cronbach and Furby (1970) titled their seminal paper on change: “How we should measure change or should we?” The last line, “or should we,” is quite interesting. Is change so difficult to measure that is not worth our time? Cronbach and Furby (1970) presented the difficulties in measuring change and presented a potential alternative. There have been many great advancements in measuring change in the past 50 years. Much of the success is due to better computing power for advanced longitudinal techniques.
David Kenny (Campbell & Kenny, 2003) discussed two of the main historical mechanisms of change. The most commonly used method was a simple difference score. With this method, we simply subtract time 2 from time 1 and then you have an indicator of how the person changes. So, if a person has a score of 100 at time 2 and a score of 99 at time 1, then he/she has a change score of 1. The simplicity of this method is one of its biggest benefits. We have an easily understandable number of how much a person has changed. There are a few issues with this type of change. First, we assume that the measure has no error. However, it is safe to assume that our measurement has error. Second, the original metric that the measure was taken on needs to be considered, as the variance is not factored into the change score. For example, we do not know if a change from 100 to 99 is a bigger or smaller change than the change from 1000 to 900 as we do not have information about variability included (either within the individual or group variability).
To account for variance, we can create a regression change score. To get a regression change score, we regress time 2 on time 1. The residual, or what is left over in time 2 after time 1, is the regression change score or what is assumed to be change. In Figure 1 below, we can see the regression change score as signified by the residual.
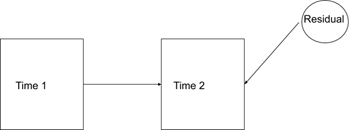
The regression change score has a benefit of accounting for variance. This method loses some of the benefit of the simplicity found in the simple change score methods. It also still has the same issue of the assumption that the measure has no error. Cross-lagged regression models also suffer from this problem that assumes the variables are measured without error.
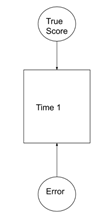
By using latent variables, we can parse variance into two components: the true score and the error of measurement. By pulling out the error, we are left with a latent variable related to our construct of interest. Saying it in the most optimistic way, we are left with a pure score.
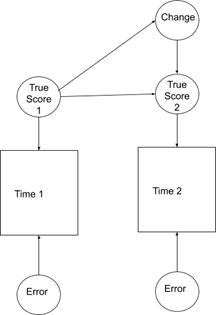
By combining latent variables with regression change scores, we can build a model that benefits from both methods. If we were to regress the latent score at time 2 on the latent score at time 1, we would be left with a change from one time to the other. We could say that this is change without the error of measurement included or pure change.
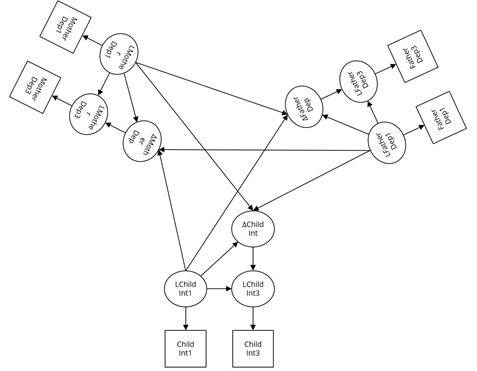
McArdle and Hamagami (2001) expanded this model with a second change process occurring in parallel (bivariate latent difference score model). These parallel change processes could influence one another. That is, we can now see when they influence each other, which is more than just saying these change processes are related to each other. Thus, we can look at leading indicators of change. In the below figure, we modeled how father’s anger influenced the child’s externalizing problems, as well as the reciprocal relationship. The main advantage of this model is that we can see the influence of one variable on the change of the other while the person is developing. That is, we can see when and how a process unfolds. Below is a figure displaying how father’s anger (Fang) and the child’s externalizing problems can each affect the other’s change. In this model, we found that each member of the dyad affects the other’s change process. That is, there is a reverberating effect of one member of the dyad leading to a worse outcome in the other, which in turn, leads to a future worst effect in the first member.
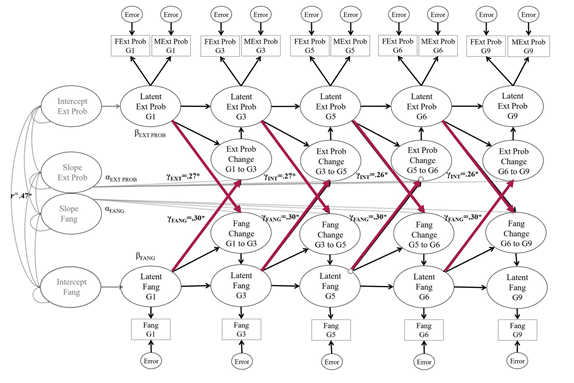
The trivariate model adds in another process (e.g., the mother influencing the father and child). We can now examine how one process is influenced by the combination of the other two. In the (simplified) figure below, we can see the mother influencing the change process in the father and child, as well as each other member influencing the other two. This type of modeling allows us to better investigate protective factors and exacerbating factors. We can also investigate how three cognitive factors influence each other over time.